From Atomic Resolution To Molecular Giants: An Overview Of Crystallographic Studies Of Biological Macromolecules With Synchrotron Radiation

Synchrotron Radiation in Natural Science Vol. 9, No. 1 – 2 (2010)

Reprinted with permission from Acta Physica Polonica A 117, 2 (2010) 257-263.

Author: Mariusz Jaskólski

Protein crystals have huge unit cells (~100 Å) filled not only with ordered protein molecules but also in about 50% with liquid water. The phase problem in protein crystallography can be solved by molecular replacement (using a suitable model molecule), by isomorphous replacement (using heavy atom derivatives), or by multiwavelength anomalous difraction (using resonant scattering of synchrotron-generated X-rays by anomalous atoms, such as Se). X-ray diffraction by protein crystals produces thousands of reflections but since the models are very complex (many thousands of atoms), paucity of data is a serious problem and stereochemical restraints are necessary. In consequence, the highest possible resolution (minimum d-spacing in Bragg’s Equation) should always be the experimental goal. Protein structures determined by crystallography are deposited in Protein Data Bank, which currently holds more than 65 000 entries. Recent methodological advancements, stimulated by a wide- spread use of powerful synchrotron sources and by structural genomics, have resulted in rapid acceleration of the structure elucidation process, and in addition help to obtain better data. Protein crystallography has produced atomic models of gigantic macromolecular assemblies, including the ribosome. It is also providing accurate targets for structure-guided development of drugs.

1. Introduction

1.1. X-ray diffraction pictures of protein crystals

When we look at the X-ray diffraction pattern of a protein crystal, we usually see an intensity-weighted reciprocal lattice with myriads of spots or reflections. But, two other things are also striking: (i) the reflections are very closely spaced and (ii) their intensity falls off rather quickly as we move away from the center, i.e., from the direction of the primary beam. The former property, i.e., small distances in reciprocal space (corresponding to small anglesθ), stems directly from Bragg’s Law, λ = 2d sinθ, and reflects the fact that protein crystals have very large unit cells in direct space (large d), necessary to accommodate the gigantic macromolecules. The latter property is the consequence of the fact that scattering of X-rays by atoms, fj, while appreciable (proportional to the number of electrons) in the forward direction, declines quickly with the scattering angleθ. An example X-ray diffraction image of a protein crystal is shown in Fig. 1. Other examples can be found in several excellent handbooks on protein crystallography, for instance [1], or in Ref. [2].

1.2. Water content in protein crystals

Usually, there is also another curious feature in the X-ray photographs of protein crystals, namely, a very strong background visible as a diffuse dark ring at a certain angle with the primary beam. This feature is due to the scattering of X-rays by disordered water molecules, which always accompany protein molecules in their crystals. The protein-to-water volume ratio is typically 1:1. This property of protein crystals is on the one hand a blessing for the protein crystallographer, because it guarantees that protein molecules even in crystalline form are in their native aqueous environment and thus they have a native structure. But it can be a curse on the other hand, because with weak, water-shielded direct protein –protein contacts the degree of molecular order can be less than perfect, which in consequence leads to a poor diffraction and to a poor structure determination. Even more importantly, the water channels in protein crystals are excellent routes for the diffusion of free radicals (generated by the ionizing X-ray radiation), which can degrade the delicate protein material very quickly.

Bulk water in protein crystals is “structured” as liquid water, i.e., we have an endless network of tetrahedrally arranged water molecules connected by hydrogen bonds, whose donor/acceptor properties fluctuate throughout the entire network. Typical O…O distances in those hydrogen bonds are 2.7 Å. This leads to a great number of 1–3 O …O vectors, whose directions, but not the length (4.4 Å), can change. Those repeated distances lead to scattering of X-rays with the intensity distribution that has a maximum at a certain angle θ.

With tuneable X-ray radiation, such as obtained in a synchrotron, the “water ring” recorded on a flat detector perpendicular to the primary beam can be bigger or smaller depending on the wavelength λ of the radiation (typically about 1 Å), but even at a constant λ we can change its radius by moving the detector in and out. It would appear that it would be advantageous to move the detector far from the crystal, because then the closely spaced diffraction spots would become well separated. While we indeed do want to achieve a physical resolution of diffraction spots on the detector, there is a different consideration, connected with another meaning of the term “resolution”, which prompts us to move the detector as close to the crystal as possible. We will explain this in the next section.

2. Fourier transformation, the phase problem, and electron density maps

To understand the reason for moving the detector as close to the crystal as possible, we must first realize that X-rays are scattered by electrons, primarily by electrons in atomic cores, but also by bonding electrons. The X-ray diffraction image is a Fourier transform of the scattering object, i.e., of the electron distribution (also called electron density) in the crystal. To be able to calculate back the information about the electron density is of a great importance to us. In chemistry, everything is explained by electrons: the nature of different atoms and bonds between them in chemical molecules. It is thus very fortunate that we have a mathematical apparatus, the inverse Fourier transform, allowing us to calculate electron density maps (Fig. 2) in the crystallographic unit cell. Electron density maps will tell us all we want to know about the chemical molecules that build up our crystal.

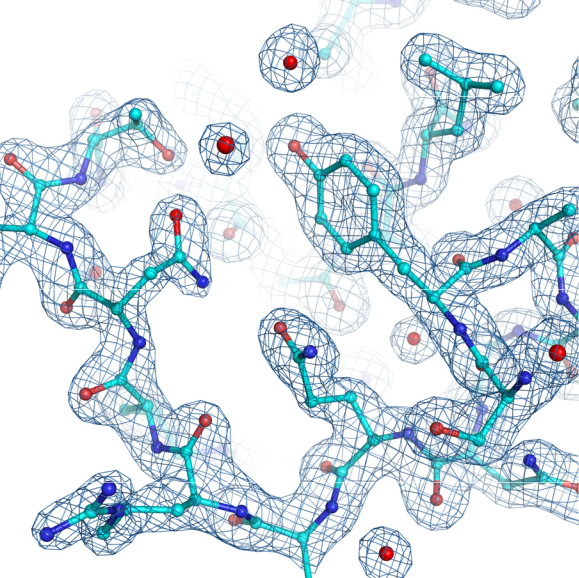
However, there is a serious obstacle on our way from the diffraction pattern to the electron density map, ρ(xyz), i.e., to the crystal structure. It is known as the phase problem because in the simple Fourier formula ρ(xyz) = ΣF(hkl)exp[-2ði(hx+ky+lz)], the complex entities F(hkl), called the structure factors, are known from the diffraction experiment with respect to their amplitudes, calculated simply as F(hkl) = √I × (hkl) (where I(hkl) is the intensity of reflection hkl), but not with respect to their phases φ(hkl).

In protein crystallography, the Fourier coefficients of electron density maps are usually of the form {(2 F_o – F_c ),φ}, where F_o is the observed structure factor and F_c is the corresponding value calculated from some atomic model. The phase φ is usually also obtained through Fourier transformation of a model, except when some experimental phase information must be generated for structures without a suitable model. In essence, the “2F_o–F_c” map can be considered as a sum of “F_o” (representing the experimental reality) and “F_o – F_c” (representing the difference between the reality and the current model) maps. Alternatively, difference “F_o –F_c” Fourier maps can also be computed to facilitate modeling aimed at model correction. In all cases where the phases are derived form an atomic model, the model will strongly influence (or bias) the appearance of the electron density maps; therefore independent experimental information is always very important.

3. Solution of the phase problem in protein crystallography

The formidable task of estimating the phases of many thousands of individual reflections can be accomplished in macromolecular crystallography on three ways, each of which relies to some extent on a peculiar inverse Fourier transform, P(uvw) = Σ F(hkl) ² exp[-2ði(hu + kv + lw)], known as the Patterson function, so named after its inventor, Arthur Lindo Patterson [3]. While the desirable function ρ(xyz) represents the distribution of atoms in the crystal unit cell, P(uvw) (which mathematically represents an autocorrelation function or the convolution of the atomic structure with its centrosymmetric image) represents the distribution of all interatomic vectors. It is clear that for large structures, such as protein structures that contain thousands of atoms, the Patterson function is astronomically complex, containing millions of vectors. But it is easily calculated and, with a judicious use, it can be of a great help. The Patterson function finds the most straightforward application in the method of molecular replacement, invented by Michael Rossmann and David Blow [4]. Here, we have an approximate atomic model of our macromolecule from which we can generate all interatomic vectors. The problem of solving an unknown crystal structure is then reduced to confronting this set of vectors with the experimental Patterson function in order to find the correct rotation and translation of the model in the unit cell of the unknown structure.

The other two methods solve the phase problem by first locating in the unit cell of a small number of special atoms (special, because they must scatter X-rays in a special way), which become the starting point for deciphering the complete structural puzzle. The classic and historically first method of isomorphous replacement, developed by the pioneer of protein crystallography, Max Perutz [5], uses a very heavy, electron-rich metal atoms, which are attached to protein molecules in an isomorphous way, i.e., without altering the crystal structure. If we are lucky, the differences in the diffraction pattern of the derivative and native crystals can reveal (via a Patterson function) the locations of the heavy atoms, which are the first, very crude, approximation of the complete structure. With one heavy atom derivative, the Single Isomorphous Replacement (SIR) approach narrows the possible solutions of the phase problem but does not give a unique solution. With more derivatives, the Multiple Isomorphous Replacement method (MIR) leads to a unique solution. An interesting variant of the isomorphous replacement method has been introduced by Dauter [6], who recommends using the simple and safe halide anions, such as Br⁻ or I⁻, instead of the highly toxic heavy metals.

The third method is based on a somewhat similar principle but it uses, as phasing markers, atoms that do not need to be very heavy but must scatter X- rays in an anomalous way. Anomalous scattering occurs when the energy of X-ray quanta is tuned to (i.e., is in resonance with) the electronic energy levels of the scattering atom. In resonance conditions, the atomic scattering factor becomes a complex quantity, f_j = f_o + f ‘ + if”, and thus introduces (through the anomalous correction if”) an extra phase shift that can be detected and used for the calculation of the unknown reflection phases. To exploit the method of anomalous scattering, we must be able to tune the wavelength of the X-ray beam, something that is possible with synchrotron radiation, and have a special atom type in our crystal structure. The normal protein atoms (C, N, O, H, and S) are not good for anomalous scattering. Therefore, a trick is usually used to introduce into the protein molecule several selenium (Se) atoms, which can be excellent anomalous scatterers of synchrotron radiation with precisely tuned λ. Typically, the experiment is conducted at several carefully adjusted wavelengths, as recommended by Wayne Hendrickson [7], which gives the method its name, Multiwavelength Anomalous Diffraction or (MAD), and allows to solve the phase problem in an algebraic way. However, with ingenuity and very accurate X-ray diffraction data, it is also possible to attempt protein structure determination using X-ray data measured in a SAD mode, at a Single wavelength, even with such weak anomalous scatterers as sulfur (in protein crystals) or phosphorus (in nucleic acids crystals) [8].

4. A digression: preparation of protein material for crystallographic studies

The trick with the Se atoms in MAD is to replace in the make- up of our protein the natural sulfur-containing amino acid methionine with its close chemical cousin containing selenium. The replacement is possible if we harness bacteria to manufacture our protein and supply them with selenomethionine (Se-Met) instead of methionine (Met). Although it sounds very bizarre, this method is a commonplace practice of genetic engineering. In fact, the majority of protein samples used nowadays for crystallographic studies are obtained not by isolation from the source organism, but recombinantly in Escherichia coli cells. Once we know the coding sequence of the protein of interest (this information is provided by genome sequencing projects, but it is also available from smaller-scale experiments), the corresponding DNA molecule (a clone) is synthesized (chemically or enzymatically using Polymerase Chain Reaction, or PCR) and introduced into a special circular DNA molecule called plasmid. Plasmids are autonomous fragments of the bacterial genome, capable of independent replication, and coding specialized traits. When a bacterial cell is transformed with an artificial plasmid, it can be turned into a factory, producing predominantly the desired protein. If additionally the bacteria is forced to grow on Se-Met medium, selenium-labeled proteins will be produced. They are then purified by chromatography and they can be used for crystallization experiments. Se-Met proteins usually crystallize and behave very much like their natural variants. In particular, bacteria tolerate selenomethionylated proteins quite well, although the situation is different with higher organisms.

5. Protein structure refinement and stereochemical restraints

Even if we solve the phase problem, the electron density map still has to be interpreted by an atomic model, and this model has to be refined. In the refinement, we calculate the structure factors using the Fourier transform F_c(hkl) = Σf_j exp[-B_j(sinθ/λ)²] exp[2πi(hx_j + ky_j + lz_j)] and introduce adjustments into our model to bring the calculated values F_c to an optimal agreement with experimental measurements, F_o. Although in principle different algorithms can be used for model optimization (for instance, the least-squares method), protein crystallographers mostly employ the maximum likelihood method [9]. Quite often, the model refinement is combined with molecular dynamics simulation at elevated temperature (this approach is callead “simulated annealing”) to facilitate better convergence and to avoid false energy minima [10].

For each atom of the model, corrections are made to its coordinates x, y, z and to a parameter, the atomic displacement parameter or the temperature factor (B), that describes the amplitude of its vibrations in the crystal lattice. Atomic vibrations, even if we assume harmonic motion, are anisotropic, and should be described by a symmetric second-rank tensor with six parameters. In most cases, there are not enough experimental data to justify such a complicated model and atomic vibrations are treated isotropically, assuming the same displacement in all directions and a spherical approximation of the vibration ellipsoid (one Biso parameter per atom).

Although it looks very straightforward, the refinement is a difficult step, mainly because of the huge number of parameters. For instance, a protein with a molecular mass of 50 kDa (average size) would consist of about 3500 non-H atoms and a simple isotropic model would require 4×3500 = 14000 parameters! Compare this with merely 8500 reflections that we would have if the resolution was poor (3 Å). Not infrequently, the number of model parameters will be close to the total number of available experimental data, making the problem barely solvable from the mathematical point of view. And, remember that in order to describe the crystal structure adequately, we also need to take care of at least some water molecules around the protein (provided, of course, that the experimental data justify such a model). To improve the situation, two approaches are possible. First, we could fix some of the model parameters or constrain them. This is, however, a dangerous trick because if a parameter is constrained wrongly, it will never be corrected. A better solution is to supplement the refinement with extra equations, called restraints, which represent our prior knowledge about the stereochemistry of the macromolecule under refinement. We can, for instance, require that the bond lengths (or angles, or other geometrical parameters) of our model have reasonable values. A list of stereochemical standards (and their uncertainties) for the use in protein structure refinement has been compiled by Engh and Huber [11] from their analysis of the structural data contained in the Cambridge Structural Database (CSD) [12]. The use of restraints has the additional appeal because the used equations approximate geometrical distortions of protein molecules using Hooke’s Law, which intuitively allows to interpret the stereochemical restraining as energy minimization.

6. Data and model resolution

The best strategy for successful refinement is, however, very simple: get more data! But how can this be achieved? Experimentally, more diffraction spots can be registered by increasing the “acceptance angle” 2θ at our detector. Through Bragg’s Equation, an increase of θmax is equivalent to a decrease of dmin, the minimum spacing of the lattice planes which still reflect the X-rays. This minimum d-value, expressed in Å, is called the resolution limit of our data. Optical considerations show that it is equivalent to the optical resolution of our model. In other words, if we collect diffraction data to 2.0 Å resolution, we can see in our electron density maps features that are more than 2 Å apart, but we will not be able to distinguish, for instance, atoms that are more closely spaced. Fortunately, we know the basic stereochemistry of our macromolecules, so it is possible to construct an atomic interpretation of the electron density map even if it does not have a true atomic resolution, but it is obvious that our main struggle should be to obtain experimental data with the highest possible resolution, because only then will we be able to see our structure atom-for-atom, refine anisotropic displacement parameters and see fine features that are not visible, or blurred by restraints, in poorly resolved maps. High-brilliance synchrotron sources of X-ray radiation are essential for a reliable measurement of the weak high-resolution data.

As a criterion for atomic resolution, 1.2 Å has been accepted [13] because 1.2 Å is the shortest covalent bond in proteins (C=O) not involving H atoms. One might think that it is a trivial thing to collect high-resolution data, a mere technicality. But this is not so because it is usually the crystal that “determines” the maximum resolution. In most cases there is no point in increasing θ max, simply because there is nothing to measure beyond a certain limit. The reasons are several: the atomic scattering factors, f_j, fall-off with 2θ quite rapidly, the atomic vibrations smear out the electrons making scattering less effective. But most importantly, protein crystals have only a limited degree of crystalline order (connected with the mixed water-protein composition of their interior) which bears directly on their ability to scatter X-rays coherently.

At very low resolution (dmin > 3.0 Å) it may be only possible to trace the main chain of the protein. At 2.7 Å, medium resolution is achieved. At this level, modeling of the solvent structure may be cautiously attempted, as the hydrogen-bonded water molecules can be already distinguished. 2.0 Å is an accepted limit of high resolution. At 1.5 Å one might start contemplating anisotropic refinement, and at 1.0 Å the weakly scattering hydrogen atoms will start to be discernible, as their C–H, N–H, etc. distances are of this order. 0.54 Å resolution is the current record achieved for a (small) protein structure [14].

7. Deposition and validation of macromolecular structures

Experimentally determined macromolecular structures are deposited in the Protein Data Bank (PDB) [15], which is a global archive of biostructural information freely and publicly available to the scientific community. When the PDB was created in 1971, there were merely seven protein structures in it. Today it stores more than 65 000 structures, most of them of proteins, and most of them determined by single crystal X-ray diffraction.

In assessing the quality of a protein structure [16], one should first check the resolution of the experimental data. The lower the dmin value is, the better. High resolution (dmin < 2.0 Å) should be always sought. The agreement with experimental data is usually measured by the crystallographic R-factor, defined as R = Σ  F_o − F_c /Σ F_o . Well refined macromolecular structures should have R < 0.2. However, one should not be tempted to reduce the R-factor at all cost, for instance by introducing model parameters that are not justified by the information content of the data (overfitting). A validation criterion to test this is R_free [17], which is calculated as the R-factor but for a small subset of randomly selected reflections which are never used for model refinement. The R_free asks the question: “how well does the model predict data it has never ’seen’ ?” Another quality-control test looks for the distribution of main-chain torsion angles (Ramachandran plot), which are seldom used as refined parameters and are, therefore, ideal for validation. Less independent but easy to calculate are r.m.s. (root-mean-square) deviations of model parameters from the stereochemical standards used as refinement restraints. Well refined medium-to-high resolution protein models should be characterized by r.m.s. deviations values for bond distances of about 0.01–0.02 Å [18].

8. Recent advancement in macromolecular crystallography

Protein crystallography is a young science, born with the publication of the first macromolecular structures by John Kendrew (myoglobin) [19] and Max Perutz (hemoglobin) [20]. In the early nineties of the previous century, it appeared that protein crystallography had already said its last word. However, since then an unprecedented surge of new data has been taking place, marking a rebirth and a new era in protein crystallography. Rapid advancements are seen in protein crystallization, in development of cryocrystallographic techniques (protein crystals are now routinely suspended in small nylon loops cooled to 100 K, Fig. 3), in the application of powerful synchrotron sources of X-ray radiation, in development of faster and more sensitive detectors, faster computers and better algorithms.

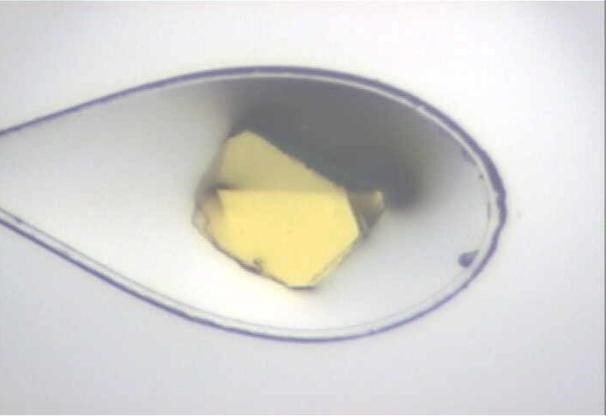Figure 3. A protein crystal (measuring about 100 μm across) suspended in a tiny loop, prepared for an X-ray diffraction experiment. The loop is used to fish out the crystal from the crystallization drop, and then to place it immediately in a stream of nitrogen gas at 100 K. In this way, the water inside and around the crystal is vitrified (i.e., becomes amorphous and does not interfere with the protein diffraction). By the same trick, the crystal is protected from drying and its structure is “stabilized” because with a lowered temperature, the thermal motions of its atoms (expressed by the B-factors) are much reduced. Most importantly, however, the solidified water component of the crystal will drastically slow down the diffusion of free radicals, which are always created on exposure to ionizing radiation, thus improving the longevity of the crystal. Courtesy of Dr. Zbigniew Dauter.[/caption]

There have been several factors contributing to the renaissance of protein crystallography, but as the most important, structural genomics initiatives should be mentioned. The need for a massive generation of structural information was a consequence of the success of genome sequencing projects (including the sequencing of the human genome), which have been generating astronomical volumes of genetic data with almost no obvious interpretation. The aim of structural genomics is then to determine in a high-throughput automated approach the three-dimensional structure of all the proteins encoded in the genome of a given organism, in order to understand their function. Contrary to classical biochemistry, the structure is studied before biochemical characterization of the target. A number of human pathogens are studied in this way, in search of new therapeutic agents.

Protein crystallography has also re-defined modern approach to drug discovery by providing precise molecular targets for accelerated, structure-guided design of new pharmaceuticals. The best known example is illustrated by the structure of HIV protease, which immediately after its elucidation [21] has become the most studied target for drug discovery. As a result, the HIV infection has been converted, within less than a decade, from a global health threat, and for an individual patient − an irrevocable death sentence, into a disease that can be treated. Today, there are eleven HIV protease inhibitors approved for the treatment of HIV infection and other proteins of the virus are being targeted as well.

Methodological advancements stimulated by structural genomics projects are also benefiting other areas of protein crystallography. For example, with improved experimental tools, there is a steady increase of the number of structures determined at atomic resolution. First atomic-resolution protein structures appeared in the PDB in mid 1980’s. Today, there are over 1 000 structures in this category. These accurate data provide us with an entirely new chemical perspective on the structure and functioning of the molecules of life.

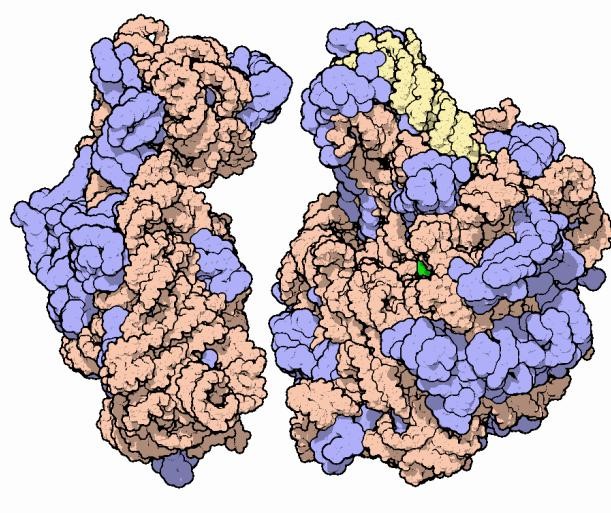
In addition to looking into macromolecular structures with a more penetrating eye, protein crystallography is also attacking problems of ever increasing complexity. Viruses are among the largest molecular systems whose atomic details have been deciphered by protein crystallography. The first crystal structures of viruses (both helical and icosahedral) were solved in 1978 [23, 24], and even then the resolution was better than 3 Å. Currently, there is a large number of virus structures in the PDB. Recently, the biggest triumph of macromolecular crystallography is the mapping of the atomic structure of the ribosomal subunits (2.4–3.0 Å) [25–27] and of the entire ribosome (2.8 Å) [28], in complex with mRNA and tRNA molecules. The scale of this achievement is illustrated by the mass of this huge macromolecular machine, used by all living cells to synthesize proteins, which is measured in megadaltons, corresponding to about two hundred thousand non-H atoms. The ribosome is composed of both proteins and ribonucleic acid molecules (Fig. 4). One of the most unexpected secrets revealed by the structure of the ribosome was that its catalytic activity is associated with the ribonucleic acid component, and not with the proteins.

9. Conclusions

Crystallography, through the study of this special solid state of matter − crystalline protein, was historically the first method to reveal for us, almost 50 years ago, the secrets of protein structure. Today, we have accumulated in the PDB an enormous amount of structural information about proteins. Crystallography is now assisted in this effort by other methods: nuclear magnetic resonance (NMR) spectroscopy, electron microscopy, and bioinformatics. But crystallography still remains the main source of information about the structure of proteins, especially in the context of structural genomics. Numerous breathtaking examples illustrate how, through unraveling macromolecular structures with increasing accuracy and at increasing level of complexity, the discipline of protein crystallography helps us to better understand the secrets of biological macromolecules, and in consequence − the secret of life.

References

1. Rupp, Biomolecular Crystallography, Garland Science, New York 2009.
2. Jaskolski, Introduction to protein crystallography for physicists, www.man.poznan.pl/CBB/PRESENTATIONS/ Jaskolski-APP.pdf , 2009.
3. L. Patterson, Z. Kristallogr. A 90 (1935) 517.
4. G. Rossmann, D.M. Blow, Acta Crystallogr. 15 (1962) 24.
5. W. Green, V.M. Ingram, M.F. Perutz, Proc. Roy. Soc. A 225 (1954) 287.
6. Dauter, M. Dauter, K.R. Rajashankar, Acta Crystallogr. D56 (2000) 232.
7. A. Hendrickson, Science 254 (1991) 51.
8. Dauter, M. Dauter, E.J. Dodson, Acta Crystallogr. D58 (2002) 494.
9. N. Murshudov, A.A. Vagin, E.J. Dodson, Acta Crystallogr. D53 (1997) 240.
10.  A.T. Brünger, J. Kuriyan, M. Karplus, Science 235 (1987)
    458.
11. R. Engh, R. Huber, Acta Crystallogr. A47 (1991) 392.
12. F.H. Allen, Acta Crystallogr. B58 (2002) 380.
13. G.M. Sheldrick, Acta Crystallogr. D46 (1990) 467.
14. C. Jelsch, M.M. Teeter, V. Lamzin, V. Pichon-Pesme,
    R.H. Blessing, C. Lecomte, Proc. Natl. Acad. Sci. USA 97
    (2000) 3171.
15. H.M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T.N.
    Bhat, H. Weissig, I.N. Shindyalov, P.E. Bourne, Nucleic
    Acids Res. 28 (2000) 235.
16.  A. Wlodawer, W. Minor, Z. Dauter, M. Jaskolski, FEBS J.
    275 (2008) 1.
17. A.T. Brunger, Nature 355 (1992) 472.
18. M. Jaskolski, M. Gilski, Z. Dauter, A. Wlodawer, Acta
    Crystallogr. D63 (2007) 611.
19. J.C. Kendrew, G. Bodo, H.M. Dintzis, R.G. Parrish, H.
    Wyckoff, D.C. Phillips, Nature 181 (1958) 662.
20. M.F. Perutz, M.G. Rossmann, A.F. Cullis, H. Muirhead,
    G. Will, A.C.T. North, Nature 185 (1960) 416.
21. A. Wlodawer, M. Miller, M. Jaskolski, B.K.
    Sathyanarayana, E. Baldwin, I.T. Weber, L.M. Selk, L.
    Clawson, J. Schneider, S.B.H. Kent, Science 245 (1989)
    616.
22.  M. Jaskolski, Postępy Biochemii 55 (2009) 15.
23.  A.C. Bloomer, J.A. Champness, G. Bricogne, R. Staden,
    A. Klug, Nature 276 (1978) 362.
24.  S.C. Harrison, A.J. Olson, C.E. Schutt, F.K. Winkler, G.
    Bricogne, Nature 276 (1978) 368.
25. F. Schluentzen, A. Tocilj, R. Zarivach, J. Harms, M.
    Gluehmann, D. Janell, A. Bashan, H. Bartels, I. Agmon, F.
    Franceschi, A. Yonath, Cell 102 (2000) 615.
26.  B.T. Wimberly, D.E. Broderson, W.M. Clemons, A.P.
    Carter, R.J. Morgan-Warren, C. Vonrhein, T. Hartsch, V.
    Ramakrishnan, Nature 407 (2000) 327.
27. N. Ban, P. Nissen, J. Hansen, P.B. Moore, T.A. Steitz,
    Science 289 (2000) 905.
28. M. Selmer, C.M. Dunham, F.V. Murphy, A. Weixlbaumer,
    S. Petry, A.C. Kelley, J.R. Weir, V. Ramakrishnan, Science
    313 (2006) 1935.